수열의 합을 간단히 나타내기 위해 우리는 기호시그마를 사용한다.
간단히 알아보자.
1부터 100까지 다 더한 것을 적어라.
1+2+3+4+5+6+7+8+9+10+11+12+생략 + 95+96+97+98+99+100을 생략없이 적을래(최소3분은 걸릴듯)
아니면 시그마라는 기호를 사용해 
1+2+3+4+5+6+7+8+9+10+11+12+생략 + 95+96+97+98+99+100 = 
그럼 시그마에 대해 알아보자.
시그마(sigma)의 정의
를 보면 K의 값은 1부터 시작해서 위에 있는 숫자 3까지 변하는 변수이네
즉 k가 1일때 1^2이고, k가 2일때 2^2이고, k가 3일 때 3^2이네 그리고 시그마 기호가 있으니깐
이 놈들을 다 더하면 되네라고 생각하면 된다.
그리고 아래에 있는 k는 꼭 1부터 시작 안해도 된다.
음수도 되고 0도 되고 아무 숫자나 다 된다.
그리고 시그마(sigma)의 아래는 k가 아니여도 된다.
시그마 아래의 문자를 다른 것으로 변경해도 뒤에 붙는 일반항의 문자도 똑같이 바꾸어주면 똑같은 값이 된다.
예제를 풀어보자.
하나는 밑이 k이고 또 하나는 밑이 m이다.
두 문자 중 한 문자를 변경해서 밑에 있는 문자를 통일 시켜 주면 된다.
그리고 명심해야 할 것이 시그마의 중심은 항상 시그마 밑에 있는 놈이 중심이다.
시그마 밑에 있는 놈말고 오른쪽에 위치한 값들은 그냥 숫자라고 생각하고 앞으로 빼버려도 된다.
시그마의 성질
주의해야 될 것이 4번 성질이다.
중심은 시그마 밑에 있는 k인데 4번 성질에는 c만 보이지 k는 보이지 않는다.
중심이 되는 변수와 그외 떨거지 상수를 구별해야만 한다.
자연수 1부터 n까지의 합은 1+2+3+......+n은 첫째항이 1, 공차가 1인 등차수열의 첫째항부터 n번째항까지의 합이므로 등차수열의 합의 공식에 의해서 1번임을 알 수 있다.
2번의 각각의 항이 자연수의 거듭제곱꼴로 나타나는 수열은 등차수열도 등비수열도 아니여서 합을 구하기가 쉽지 않다.
이 때 항등식의 성질을 이용해서 유도할 수 있다.
항등식 (k+1)^3 - k^3=3k^2+3k+1의 양변에 k=1,2,3.....,n을 차례대로 대입하면 아래와 같다.
계산하면 좌변은 다 안녕하고 (n+1)^3 - 1^3만 남고 우변은 정리하면 아래와 같다.
3번은 역시 항등식 (k+1)^4-1^4=4k^3+6k^2+4k+1으로 유도가능하다.
'수학 > 수학공식' 카테고리의 다른 글
| 삼각함수 공식들 (1) | 2017.09.04 |
|---|---|
| 미분 공식들 (2) | 2017.09.04 |
| 쌍곡선 함수 공식 모음 (0) | 2017.09.02 |
| 적분공식들 (4) | 2017.09.01 |
| 로그의 정의와 성질 및 상용로그 계산 (4) | 2017.02.24 |
| 절대값 계산하기 (1) | 2017.02.19 |
| 평균값이 왜 이리 틀리지 이상하네? (0) | 2017.02.18 |
| 헤론의 공식 증명 (5) | 2017.01.22 |
| sinx, cosx, tanx, logx의 값들 (1) | 2012.11.14 |













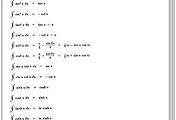

댓글