간단히 머리속으로 암산이 되는 계산.
즉 구구단을 제외하고는 바로 옆에 메모지와 필기구가 있어도 계산기나 스마트폰을 먼저 찾는다.
요즘은 어떤지 모르지만 항상 대학 시험시간에 계산기는 필수였다.
컬투쇼 계산기 = https://www.youtube.com/watch?v=54ytCru5M0U
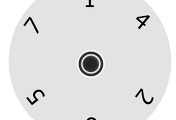
UN숫자는 평소에 항상 접하는 계산기나 스마트폰의 다이얼 버튼, 달력 등에 있는 숫자들을 U자 혹은 N자로 눌렀을 때 나오는 숫자로
8569, 4125, 5236, 7458, 9647, 1452, 5896 등이 있다.
U자나 N자의 숫자를 누르고 나누기 11을 해보면 정확히 소수점없이 정수로 딱 나누어 떨어지는 것을 알 수 있다.
그럼 숫자 11로 나누어 떨어지니 UN숫자는 11의 배수가 된다는 사실이다.
11의 배수는 어떻게 할 수 있을까?
임의의 숫자가 있을 때 각 자리 숫자에 +-+-+-+- 부호를 붙여 계산한 결과값이 0 혹은 11(11, 22, 33…)의 배수일 때 임의의 숫자는 11의 배수가 된다.
예컨대
123123이 11의 배수일까?
+1-2+3-1+2-3 = 0
따라서 123123은 11의 배수이다.
실제로
123123 = 11 × 11193
으로 11로 나누어 떨어진다.
위의 UN숫자를 일반화 해보자.
왼쪽 하단의 수를 x라고 두면
오른쪽으로 갈수록 +1만큼, 위로 갈수록 +3만큼 크지는 것을 알 수 있다.
위의 그림을 U자로 표시하면
x+3, x , x+1, x+4가 되고
+(x+3) - (x) + (x+1) - (x+4)
= 0
이 됨을 알 수 있다.
N자 역시
+x - (x+3) + (x+4) - (x+1)
= 0
이 나옴을 알 수 있다.
요컨대 11의 배수 판정법은
각 자리수에 +-+-+-+-를 넣어주고 합한 값이 0혹은 11의 배수의 값이 나올 때 11의 배수가 된다.
2017/08/17 - [수학/수학이야기] - 수학 트릭 남아있는 숫자 맞추기
배수판정법
2의 배수 판정법 : 끝자리가 0, 2, 4, 6, 8 짝수
3의 배수 판정법 : 각 자리 수의 합이 3의 배수
4의 배수 판정법 : 끝 두 자리 수가 4의 배수
5의 배수 판정법 : 끝자리가 0 또는 5
6의 배수 판정법 : 2의 배수이면서 동시에 3의 배수
8의 배수 판정법 : 끝 세 자리 수가 8의 배수
9의 배수 판정법 : 각 자리 수의 합이 9의 배수
7은 좀 다른데 끝 자리수만 분리 한 후 나머지수-끝자리*2의 결과값이 0 또는 7의 배수이면 7의 배수이다.
출처: http://elwlsek.tistory.com/718 [어짜고 저짜고 뭐라고]
배수판정법
2의 배수 판정법 : 끝자리가 0, 2, 4, 6, 8 짝수
3의 배수 판정법 : 각 자리 수의 합이 3의 배수
4의 배수 판정법 : 끝 두 자리 수가 4의 배수
5의 배수 판정법 : 끝자리가 0 또는 5
6의 배수 판정법 : 2의 배수이면서 동시에 3의 배수
8의 배수 판정법 : 끝 세 자리 수가 8의 배수
9의 배수 판정법 : 각 자리 수의 합이 9의 배수
7은 좀 다른데 끝 자리수만 분리 한 후 나머지수-끝자리*2의 결과값이 0 또는 7의 배수이면 7의 배수이다.
출처: http://elwlsek.tistory.com/718 [어짜고 저짜고 뭐라고]
배수판정법
2의 배수 판정법 : 끝자리가 0, 2, 4, 6, 8 짝수
3의 배수 판정법 : 각 자리 수의 합이 3의 배수
4의 배수 판정법 : 끝 두 자리 수가 4의 배수
5의 배수 판정법 : 끝자리가 0 또는 5
6의 배수 판정법 : 2의 배수이면서 동시에 3의 배수
8의 배수 판정법 : 끝 세 자리 수가 8의 배수
9의 배수 판정법 : 각 자리 수의 합이 9의 배수
7은 좀 다른데 끝 자리수만 분리 한 후 나머지수-끝자리*2의 결과값이 0 또는 7의 배수이면 7의 배수이다.
11의 배수는 각 자리수 앞에 +-+-+-+-… 부호를 넣은 후 합한 결과값이 0 또는 11의 배수일 때 11의 배수가 된다.
'수학 > 수학이야기' 카테고리의 다른 글
| 시속을 초속으로 변환하기(속도변환) (5) | 2018.01.21 |
|---|---|
| 원소주기율표 한 눈에 확인하는 사이트 (0) | 2017.10.28 |
| (삼각형 문제) 한 칸이 어디로 사라진 것일까? (1) | 2017.10.03 |
| 숫자 4를 4번 이용해서 1~10까지 만들어보기 (1) | 2017.08.24 |
| 수학 트릭 남아있는 숫자 맞추기 (0) | 2017.08.17 |
| 돌고 도는 순환수(cyclic number) (0) | 2017.08.16 |
| 숫자 9를 4번 사용해서 0~10까지 만들어 보기 (2) | 2017.08.09 |
| 울프람알파 적분, 미분식 입력방법 (0) | 2017.06.27 |
| 날짜만 가지고 무슨 요일인지 알 수 있다. (3) | 2017.06.26 |







댓글