우리는 어릴 때부터 선생님이나 부모님에게 혼나가면서 구구단을 외운다.
불행 중 다행인 것은 인도에서는 19단까지 암기를 하고, 일부 미국같은 나라들은 12단까지 외우는 것에 위안을 삼아야 하는 것일까?
그렇다면 과연 9단 말고 19단까지 외우고 있는 것이 수학을 하는 데 얼마나 큰 도움이 될까?
물론 큰 도움은 되겠지만 이로 인해 오히려 수학이 더 무서워지는 아이들도 나올 수 있을 것 같다.
구구단 외에 자주 사용되는 제곱수나 자신의 직업상 자동적으로 암기되어져 버린 곱셈의 수도 있을 것이다.
그럼 19×19단을 외우지 않고 몇 초만에 답이 나올 수 있을까?
닶은 당연하다.
간단히 수학의 항등식의 성질을 이용해 조금 익숙해지면 19단의 계산은 쉽다.
먼저 항등식(恒等式)이 무엇인지 알아야 한다.
X의 값에 관계없이, 즉 X가 1이 되던, 2가 되던, 1억이 되던, 1004가 되던 무슨 값을 넣어도 항상 항상 항상 좌우변의 식이 같은 등식을 말한다.
다시 적으면
1. X의 값에 관계없이 항상 성립
2. 임의의 X의 값과 상관 없이 성립
3. 어떤 X의 값에 대햐여도 성립
4. 모든 X의 값에 대하여 성립 일 때 (좌변)=(우변)을 항상 만족하는 등식이 항등식다.
간단한 예로 아래 식을 보자.
X의 값을 1을 넣으면 좌변과 우변은 각각 1+1=1+2-1이 되고 2=2가 된다.
다음 X에 내맘대로 꼴리는 숫자가 뭐가 있지 X를 18이라고 하면 좌변과 우변은 각각 18+1=18+2-1이 되고 19=19가 된다.
즉 X의 값에 내 맘대로 꼴리는 숫자 아무것이나 랜덤으로 집어 넣어도 항상 좌변과 우변의 같다는 것을 알 수 있다.
자 그럼 항등식을 이용해 19×19단을 알아보자.
먼저 아래의 곱셈공식을 보자.
(단 X=10이고 a,b는 0과 9사이의 자연수이다.)
X가 10이라고 했으므로 넣어보자.
그럼
가 된다.
얼핏 보면 두 수의 합(a+b)과 곱(ab)을 알면 왠지 금방이라도 답이 나올 것 같다.
예컨대
12*17을 해보자.
가 된다.
빨간 박스의 두 수는 더하고 두 수의 일의 자리인 파란 박스는 곱해서 한 자리 뒤에 위치시키고 두 수를 더하면 답이 된다.
아래와 같이 바로 계산을 해도 마찬가지이다.
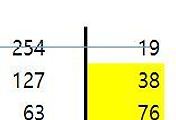
예제 하나 더 가보자. 17*19을 암산해보자.
먼저 17과 9를 더한다.
26가 나온다.
7과 9을 곱하면
63이 나온다.
따라서 260 + 63 = 323이 나온다.
익숙하지 않지만 몇 개 정도 위와 같은 방법으로 풀이를 해보면 암기보다는 더 쉽고 편한 방법이라고 생각든다.
'수학 > 수학이야기' 카테고리의 다른 글
| 울프람알파 적분, 미분식 입력방법 (0) | 2017.06.27 |
|---|---|
| 날짜만 가지고 무슨 요일인지 알 수 있다. (3) | 2017.06.26 |
| WolframAlpha setup(PC 울프람알파 설치방법) (4) | 2017.05.11 |
| 집합 이야기 (0) | 2017.03.05 |
| 포커 게임 패의 확률 (4) | 2017.02.24 |
| 구구단 없는 곱셈법 (2) | 2017.02.21 |
| 이자와 대출 등차수열과 등비수열 (1) | 2017.02.20 |
| 상대방의 마음을 읽는 수학 (1) | 2017.02.20 |
| 두 물체의 무게중심은 어디일까? (1) | 2017.02.18 |






댓글